| Otázka č. 1: | Riešte v N rovnicu 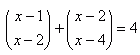 : : |
| 5 |
| 8 |
| 4 |
| 7 |
|
| Otázka č. 2: |
| Počet variácií druhej triedy z 10 prvkov je: |
| 90 |
| 100 |
| 19 |
| 20 |
|
| Otázka č. 3: |
| Koľko 6-ciferných čísel možno zostaviť z číslic 1, 3, 5, 6, 7, 9, ak sa nemajú číslice opakovať? |
| 360 |
| 1440 |
| 5670 |
| 720 |
|
| Otázka č. 4: |
| Na prestížne ocenenie Zlatá kamera bolo nominovaných 10 filmov. Každý divák vyberie tri z nich a na hlasovacom lístku navrhne jeden na 1. cenu, jeden na 2. cenu a jeden na 3. cenu. Najviac koľko rôzne vyplnených hlasovacích lístkov môže porota teoreticky dostať? |
| 360 |
| 1000 |
| 120 |
| 720 |
|
| Otázka č. 5: |
| Z koľkých prvkov môžeme vytvoriť 30 variácií druhej triedy? |
| 4 |
| 5 |
| 7 |
| 6 |
|
| Otázka č. 6: |
| Umocnite výraz (2a3 - 5)4 : |
| 2 a12 - 80 a9+ 300 a6 - 500 a3 + 625 |
| 16 a7 - 160 a5+ 600 a3 - 1000 a + 625 |
| 16 a12 - 160 a9+ 600 a6 - 1000 a3 + 625 |
| 16 a12 + 160 a9+ 600 a6 + 1000 a3 + 625 |
|
| Otázka č. 7: |
| Z 30 študentov 4.A triedy je 10 vyznamenaných. Koľkými spôsobmi môžeme spomedzi všetkých študentov v triede vybrať piatich, ak medzi nimi majú byť práve dvaja vyznamenaní? |
| 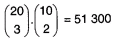 |
|  |
| 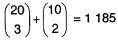 |
| 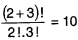 |
|
| Otázka č. 8: |
| Počet variácií tretej triedy z 5 prvkov s opakovaním je: |
| 125 |
| 15 |
| 60 |
| 75 |
|
| Otázka č. 9: |
Kombinačné číslo 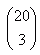 sa rovná: sa rovná: |
| 520 |
| 1320 |
| 380 |
| 1140 |
|
| Otázka č. 10: |
Štvrtý člen binomického rozvoja výrazu 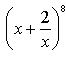 je: je: |
| 56 x2 |
| 224 x2 |
| 448 x2 |
| 224 x3 |
|
| Otázka č. 11: |
| Ktorá z rovníc je pravdivá? |
| 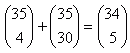 |
| 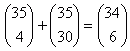 |
| 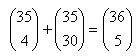 |
| 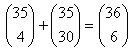 |
|
| Otázka č. 12: |
| Kódom na trezore je slovo (postupnosť písmen, ktorá nemusí mať význam) pozostávajúce zo šiestich rôznych písmen. Prvé tri písmená sú spoluhlásky z množiny {B, C, D, F, G}, ďalšie tri písmená sú samohlásky z množiny {A, E, I, O, U, Y}. Koľko rôznych slov prichádza do úvahy ako kód na trezore? |
| 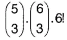 |
| 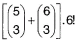 |
| 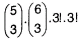 |
| 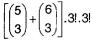 |
|
|